 Purdue News
Purdue News
 Purdue News
Purdue News
December 1997
|
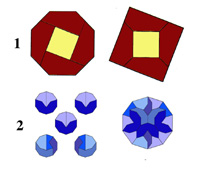
For example, the book shows how to cut an octagon into five pieces and rearrange them into a square, and how to turn a star into a pentagon.
"This book has been great fun to write, in part because I let my curiosity lead the way," Frederickson writes in the preface. "The intended audience is anyone who had a course in high school geometry and thought that regular hexagons were rather pretty."
The 320-page book, published in November by Cambridge University Press, contains more than 500 illustrations. It sells for $34.95.
In the book, Frederickson explains solution methods, assuming only a basic knowledge of high school geometry, then poses puzzles to solve. He also introduces the people -- famous and obscure -- who have worked on these problems, traveling from the palace school of 10th century Baghdad to the mathematical puzzle columns in turn-of-the-century newspapers.
A discussion of each problem highlights the techniques and their underlying mathematical properties, and is accompanied by numerous diagrams.
Solving dissection puzzles is a great way to teach lessons about the mathematical concept of area, Frederickson says.
"Shapes can be cut up and rearranged, but the total area does not change," he says. "Dissections also can be used to learn about various types of symmetry and patterns. Some of the dissections in the book also can be used to illustrate things like the Pythagorean theorem, which illustrates the relationship between the lengths of the sides in a right-angle triangle."
Frederickson first became interested in mathematical dissections as a high school student when his parents bought him a book on the subject by Harry Lindgren. After graduating from Harvard with a bachelor's degree in economics, Frederickson taught junior high mathematics for several years, and he found ways to use the dissections to help motivate students.
"At some point, I figured out how to improve one of the dissections by finding a solution with one fewer piece," he says. "I started playing with these puzzles more and more, and soon found more improvements."
Frederickson began corresponding with Lindgren, who was encouraging and supportive. In 1972, Frederickson published an appendix to Lindgren's original book, which appeared in a paperback version. Soon after that, he embarked upon his career in academia, and set aside his interest in dissections.
In 1991, he received a letter from Martin Gardner, an author who was revising a book on mathematical games.
"He wrote asking me 'What's new in dissections?' and that prompted me to pull all of this information out of the closet and begin thinking about them again," Frederickson says. "A few years later, when my wife and children went to Europe for a few weeks, I began writing the book."
The book includes hundreds of dissections, some of which appeared in newspaper and magazine columns during the first part of the century, and includes biographical information on the people who have made a contribution to this area. In addition, the book contains many new unpublished dissections by Frederickson and others.
Though most of the book is based on high-school-level mathematics, Frederickson used simple but precise graphics throughout the book so that readers of all levels can skim through even the most difficult sections.
"On the other hand, if a reader gets intrigued with a topic and wants to follow up on it, I have provided additional comments and references in the afterword," Frederickson says.
Source: Greg Frederickson, (765) 494-6016; e-mail, gnf@cs.purdue.edu; Web, https://www.cs.purdue.edu/people/gnf
Writer: Susan Gaidos, (765) 494-2081; e-mail, susan_gaidos@purdue.edu
Purdue News Service: (765) 494-2096; e-mail, purduenews@purdue.edu
Caption 1:
This illustration shows how to dissect an octagon into five pieces to make a square.
The octagon and square also illustrate four-fold symmetry, as the pieces outside
the centers are identical and each figure has a square at its center, The octagon
also depicts rotational symmetry: If it is rotated 90 degrees, it will exactly match the original
figure. (Purdue News Service illustration edited by Shirley Yeung.)
Caption 2:
This illustration shows how five 10-sided figures can be cut to make one large decagon.
The 17-piece dissection first appeared in 1974. (Purdue News Service illustration
edited by Shirley Yeung.)
Color illustrations, electronic transmission, and Web and ftp download available.
Graphic ID: Frederickson.Dissection
Download here.
 To the Purdue News and Photos Page
To the Purdue News and Photos Page