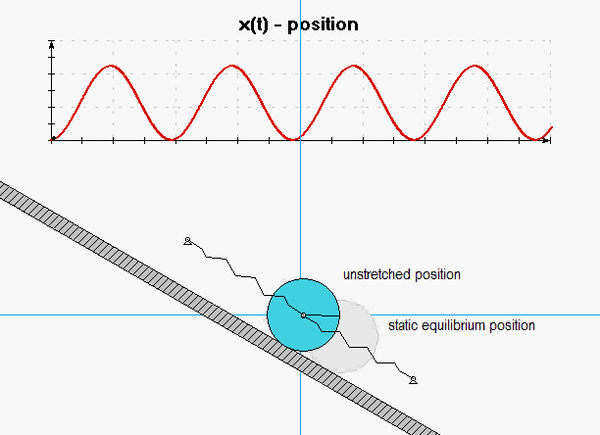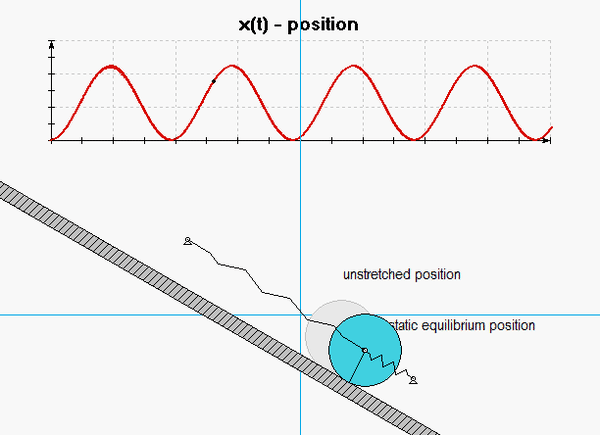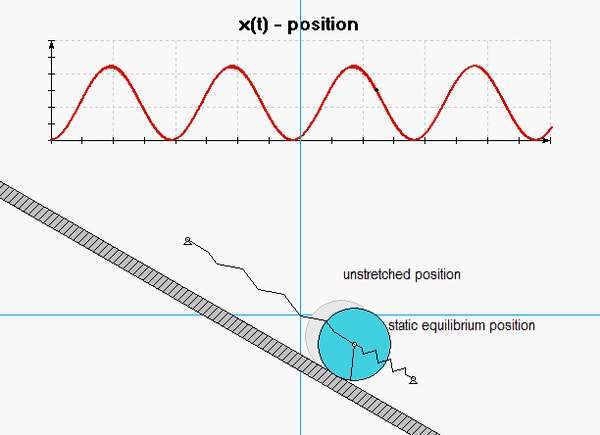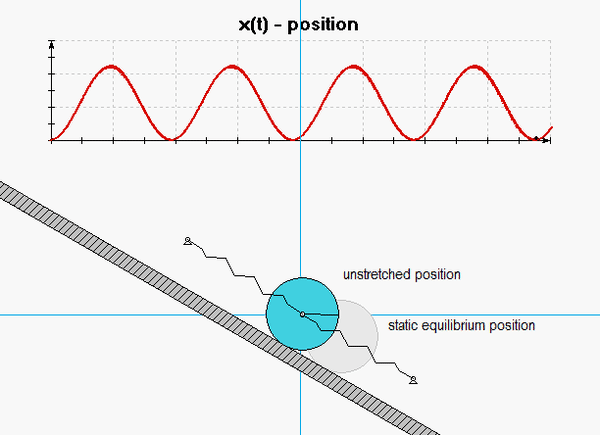
A homogeneous disk of mass m and outer radius R rolls without slipping on an inclined surface, with the center of the disk supported by two springs, as shown below.
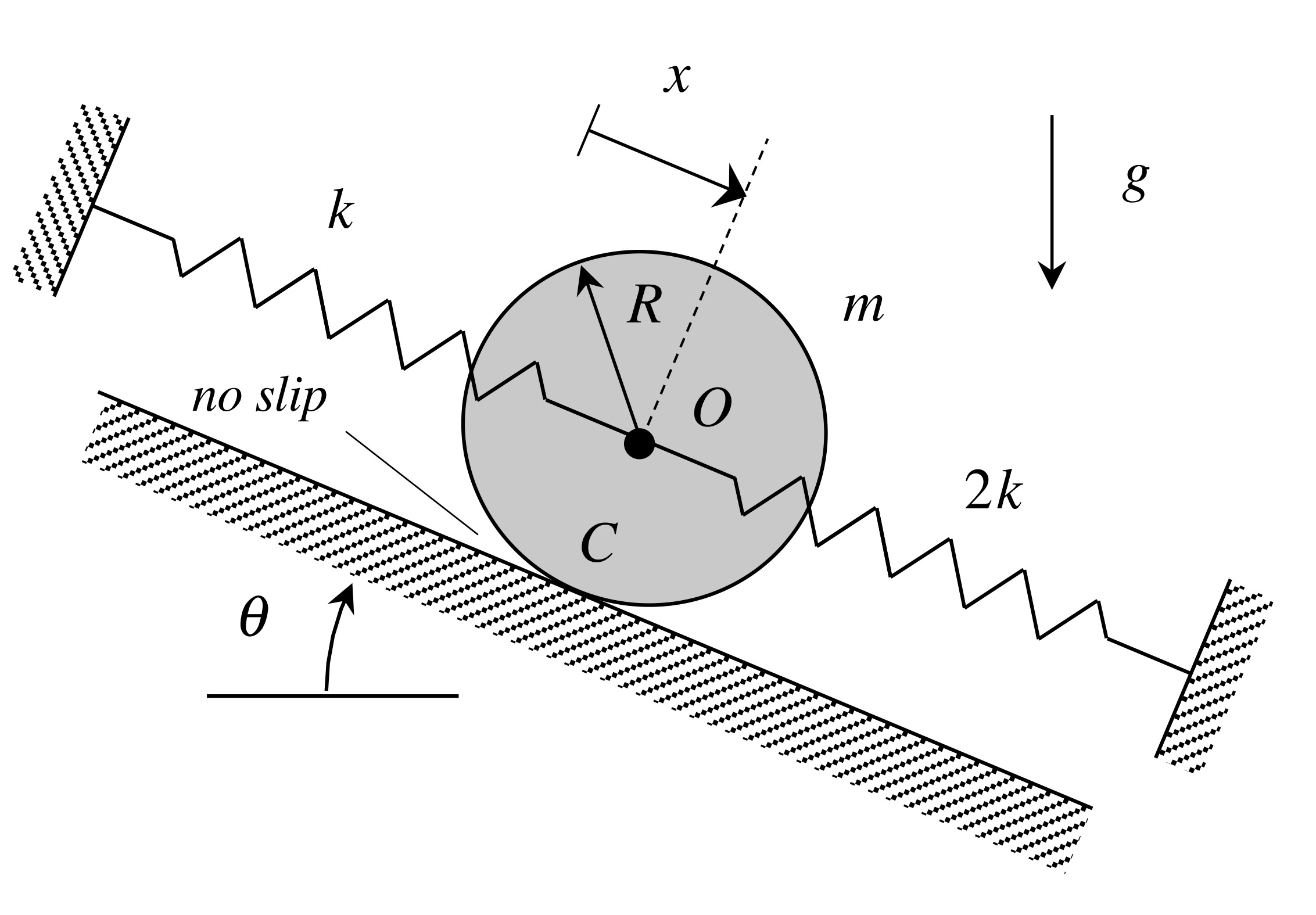
Say we let x represent the displacement of the center O from where the springs are unstretched. The dynamical equation of motion (EOM) in terms of the coordinate x is shown below. As we can see, the resulting EOM is inhomogeneous.
From this EOM, we also see that the static equilibrium position of O is given by: xstatic = mg sin(theta)/3k. That is, if the disk were placed at a position of x = xstatic, the disk remains there in equilibrium.
Suppose that we choose a new coordinate of z = x - xstatic , which represents the motion of O relative to the static equilibrium position. The EOM in terms of his new coordinate is shown above to be homogenous.
Physical interpretation
Shown below is an animation from a simulation of the free response of the system with initial conditions of x(0) = x_dot(0) = 0. The red curve shown below is the response of the system, x(t). Note that the response is harmonic with a non-zero mean value, as expected. From the above analysis, we know that the frequency of response is given by omegan = sqrt(2k/m). Relevant to our discussion above is that the oscillations occur about the static equilibrium position of the disk (shown in grey). The motion about that position is z(t), which has a zero mean value.