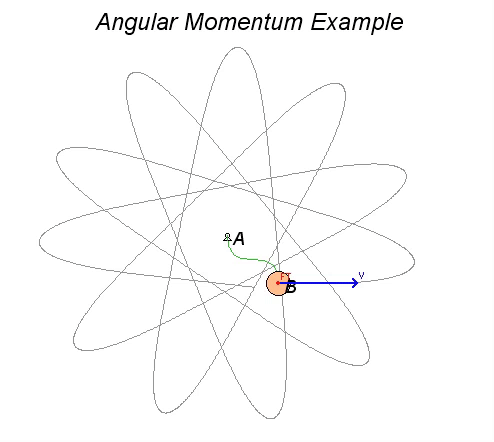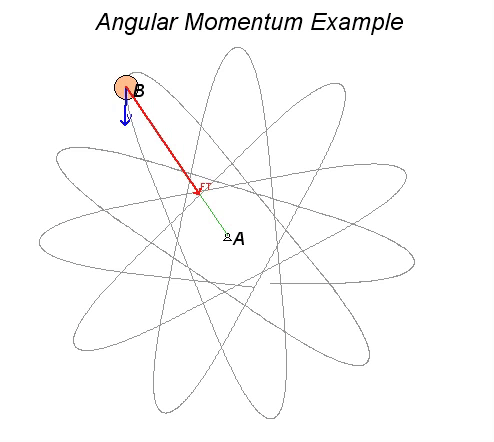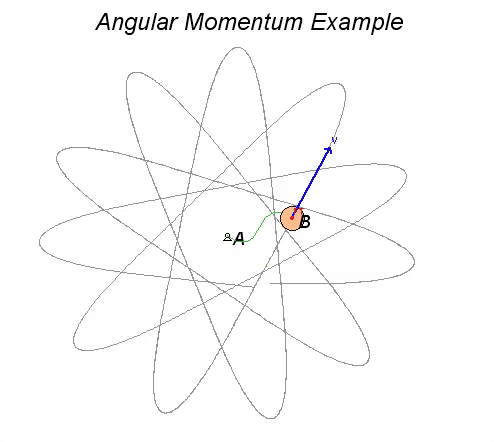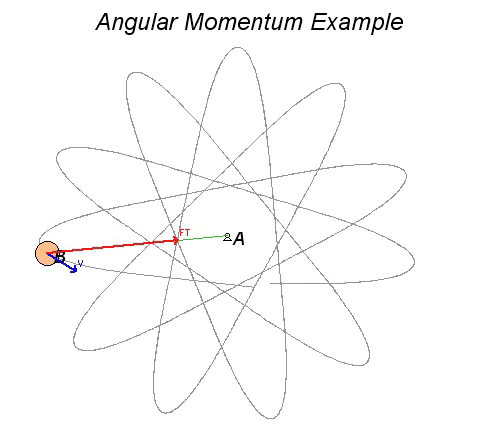
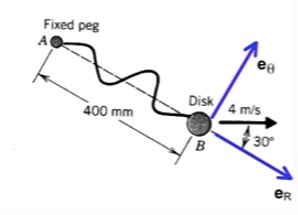
Consider Example 4.D.3 from the lecture book. Here, a disk of mass is tied to a rubber band, with the opposite end of the rubber ban being tied to a peg at A. The disk is set into motion at the position shown in a HORIZONTAL plane. We desire to calculate and visualize the velocity of B as it moves in its plane of motion.
Observations
- As the disk moves through its motion, the only force acting on it in its plane of motion is the tension force from the rubber band. This rubber band force, when non-zero, points toward the fixed peg at A.
- Since this force acts through A, the moment about point A due to the force is always zero. Consequently, the angular momentum of the disk about point A is conserved (constant).
- Furthermore, energy is conserved for the disk/rubber band system (no non-conservative forces do work on the system).
- Using both conservation of angular momentum and conservation of energy, we can solve for the radial and transverse components of velocity for B. This solution is provided in the lecture example video for Example 4.D.3 on the course blog.
Watch the animation below from the simulation of the motion of the disk, where the red vector is the rubber band force on the disk, and the blue vector is the velocity of the disk. Let θ_dot represent the angular velocity of the line AB as the disk moves. The angular momentum of the disk about A is HA = m*R2*θ_dot, where R is the distance between A and B. This equation says that as R increases (B moves outward from A), the angular velocity θ_dot must decrease. This is true regardless of whether the rubber band is stretched or slack. You can observe this in the animation below.
Note that we are able to describe a rather complicated motion of the disk using two rather simple equations.