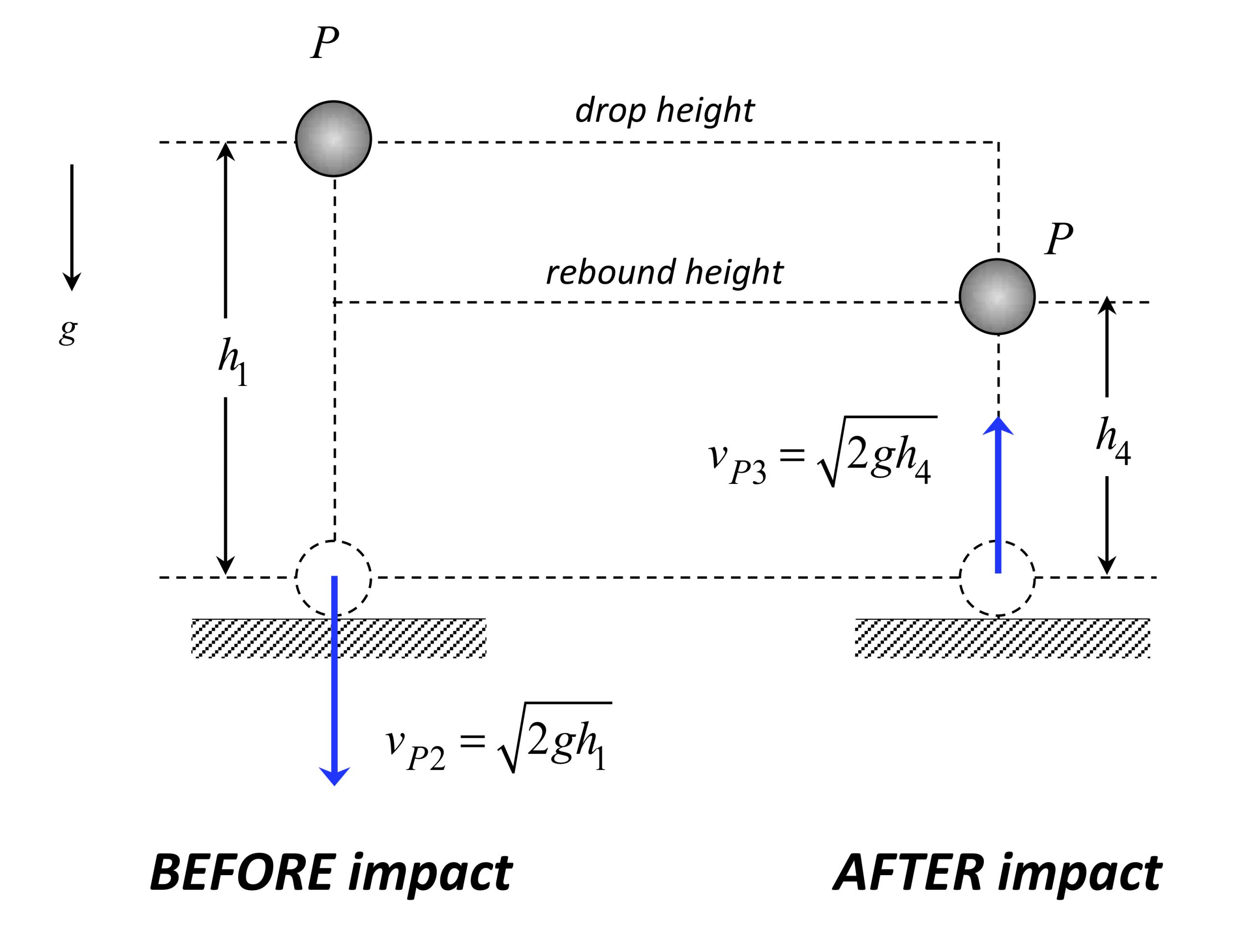
Particle P is dropped from rest from a height of h1 above a fixed floor. Immediately prior to impact with the floor, P has a speed of vP2. After impact, P has a rebound speed of vP3 eventually reaches a maximum height of h4 before falling back down.
Energy analysis
Using conservation of energy, we can show that: vP2 = - √(2gh1). In a similar way, conservation of energy gives us that: vP3 = √(2gh4).
Determination of the coefficient of restitution (COR)
Based on the definition of the COR, we can write:
e =-vP3/ vP2 = √(h4/h1)
The above result says that we can extract the COR for an impact during a drop test by taking the square root of the ratio of the rebound height to the initial drop height.
Drop test results
Consider the animation of a drop test shown below. The ball is dropped from a height of h1 = 10 inches. The maximum height after the first impact is seen to be h4 = 4.95 inches. What is the COR for this impact?

Influence of COR on rebound height

Six balls are dropped from the same initial height h1. These balls have varying values of the COR, ranging from e = 0 to e = 1. The above shows an animation of the simulation results for these drop tests. Recall from above that the rebound height h4 is given by: h4 = e2 h1. From this, we see that the rebound height decreases in a quadratic fashion as the COR is decreased. Low values of COR show rapid reduction of the rebound heights.
Questions:
- Based on our analysis, for a given value of COR of e > 0, how many impacts are required before the ball comes to complete rest? (Be careful with your answer...)
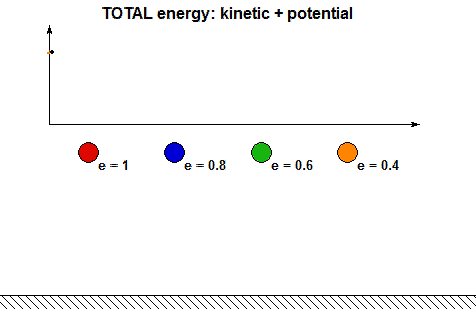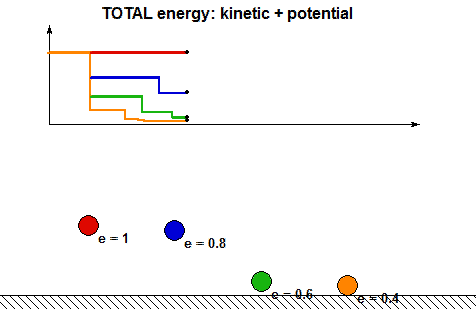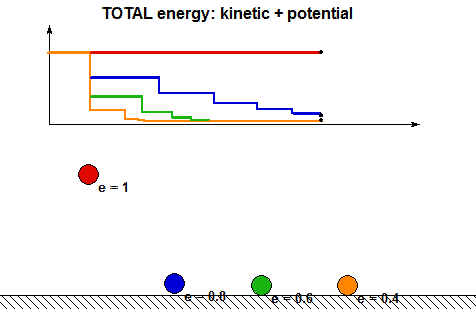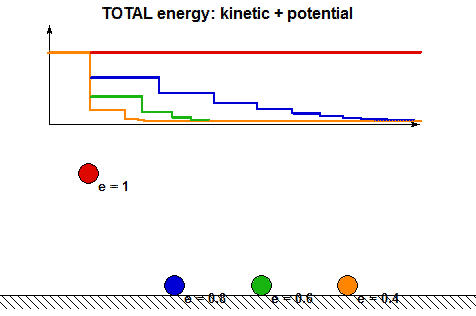
- It is clear from the above animations that energy is lost with each impact. How is the energy lost related to the COR? Using the analysis above, we can show that the ratio of total mechanical energy before impact, E2, to the total mechanical energy after impact, E3, are related through: E3 = e2E2. Can you see this in the following animation showing the energy changes during each impact for four values of COR e?