Discussion and hints:

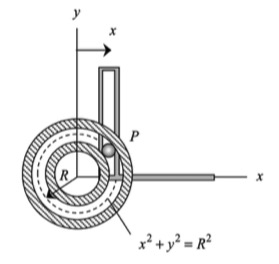
In this problem, the xy-Cartesian components are constrained through the equation of the path of P:  x² + y² = R².  The x-component of the position is an explicit function of time. Finding the time derivatives of x is done through simple time differentiation of x = b sinωt. The derivatives of y with respect to time is found through the time differentiation of the constraint equation: x² + y² = R². Please review the examples worked out in lecture to assist you in this differentiation.

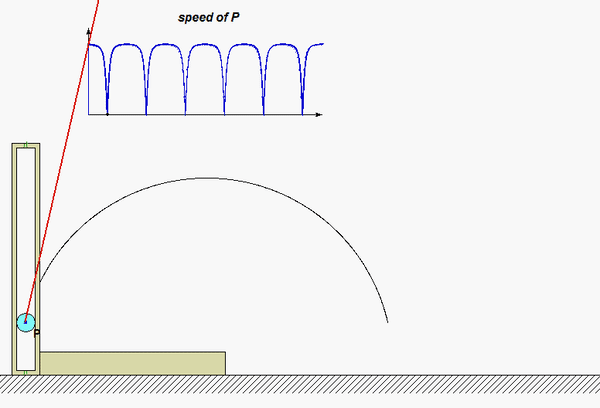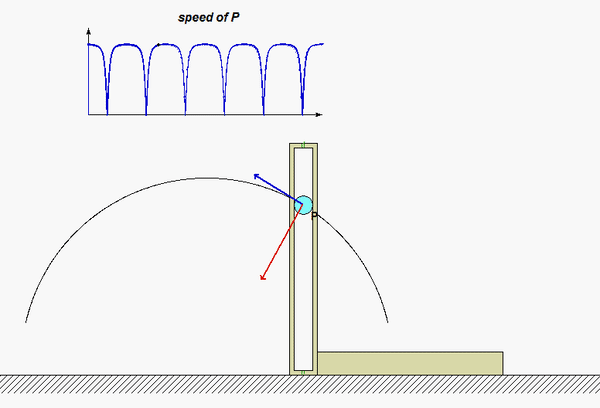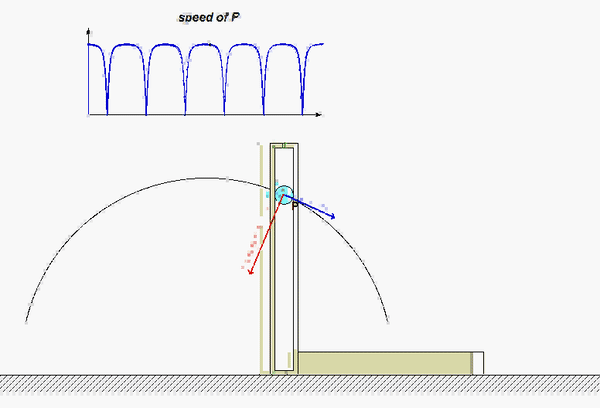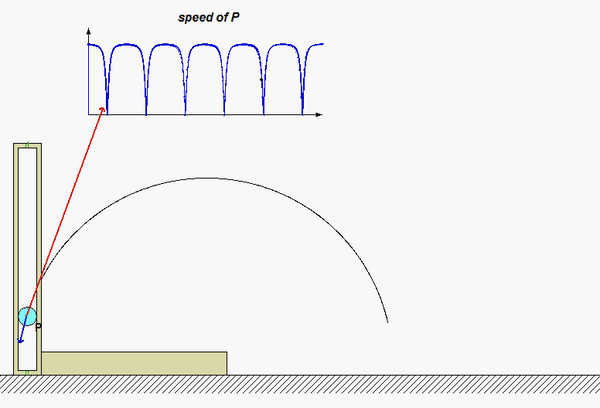
The results of this analysis are shown in the animation below. From this animation, we see that the velocity of the P (shown in BLUE) is always tangent to the path of P. The acceleration (shown in RED) is not quite so simple: it has components both tangent and perpendicular to the path; however, the component perpendicular to the path always points inward on the path. Both of these observations are consistent with what we see in the next lecture when we develop the expressions for velocity and acceleration in terms of their PATH components.

Any questions??