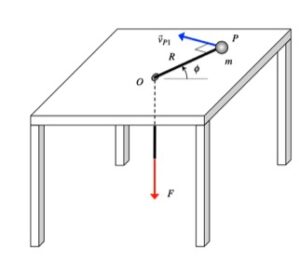
NOTE: Please use F = 2000 N in this problem.
Any questions?? Please ask/answer questions regarding this homework problem through the "Leave a Comment" link above.
Discussion and hints
Recall the following four-step plan outline in the lecture book and discussed in lecture:
Step 1: FBDs
Draw a free body diagram of P.
Step 2: Kinetics (angular impulse/momentum and work/energy)
Note that all forces acting on P in the plane of the table point toward the fixed point O. What does this say about the angular momentum of P about point O? Also, consider the work/energy equation for P.
Step 3: Kinematics
The kinematics of P are best written in terms of polar coordinates R and φ.
Step 4: Solve
Solve for the R and φ components of velocity of P from these equations.