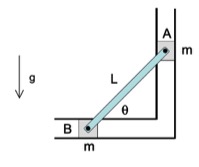
NOTE: All surfaces are smooth. Unfortunately, this information was omitted from the problem statement.

Any questions?? Please ask/answer questions regarding this homework problem through the "Leave a Comment" link above.

---

Discussion and hints

 

 

Recall the four-step solution process:

STEP 1 - FBD: Draw a SINGLE free body diagram (FBD) of the system including Block A, Block B and the rigid bar. From this, determine which forces do non-conservative work on this system, if any.
STEP 2 - Kinetics:  Write down the work/energy equation.
STEP 3 - Kinematics: Consider the location of the instant center for bar AB. This will be the key to the kinematics that you need to solve this problem.
STEP 4 - Solve

__________________________