Any questions?? Please ask/answer questions regarding this homework problem through the "Leave a Comment" link above.
Discussion
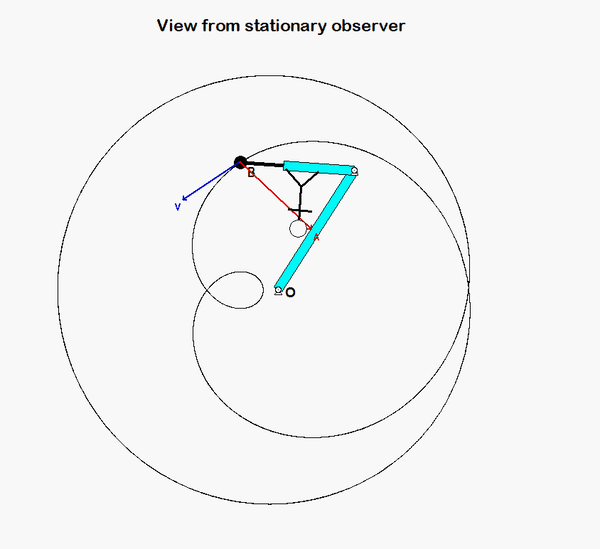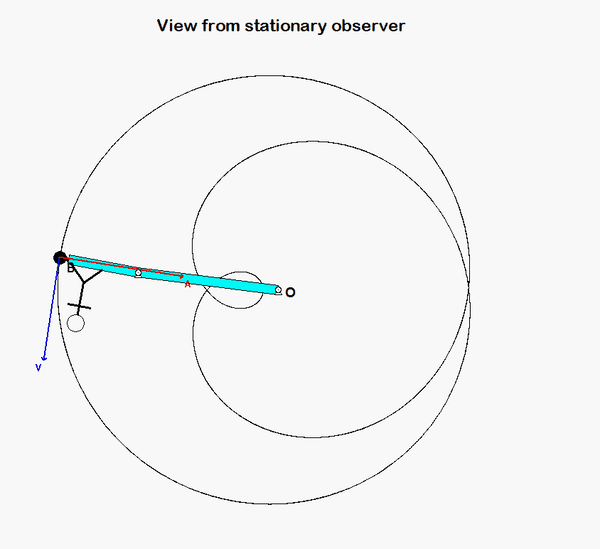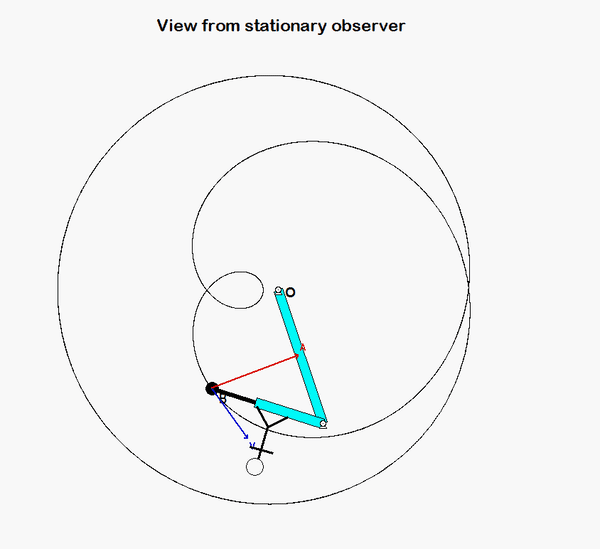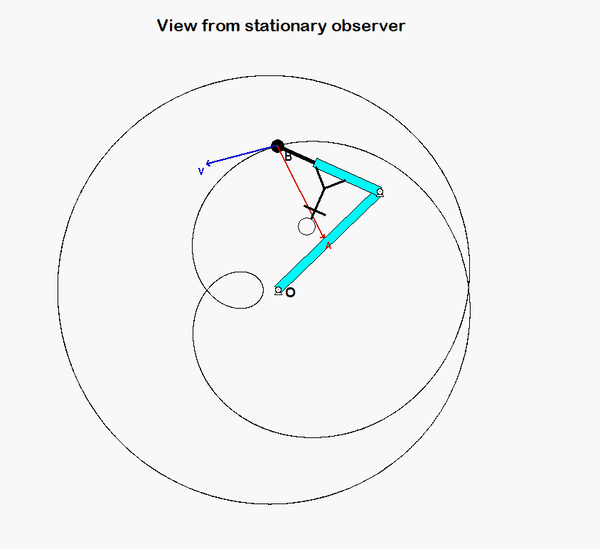
An animation from the simulation of the motion of the robotic arm system is shown above for a fixed observer. The motion of end-effector B is quite complicated, as can be seen. However, if we attach an observer to section AD of the end link of the arm, the observed motion of B is greatly simplified. In fact, the observer simply sees a back-and-forth motion of B in the x-direction, as shown in the animation below.
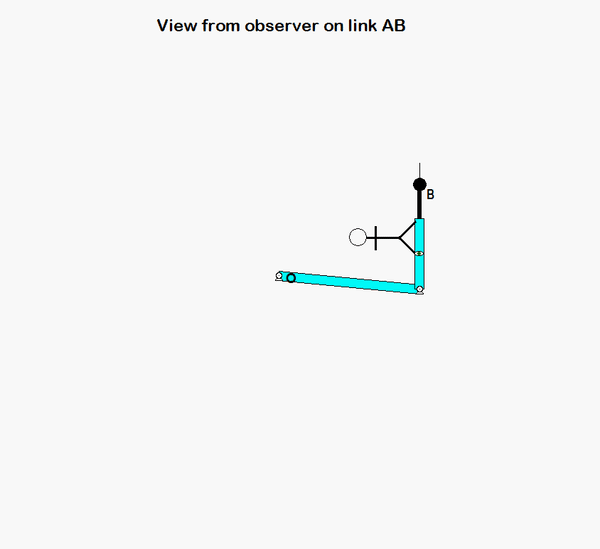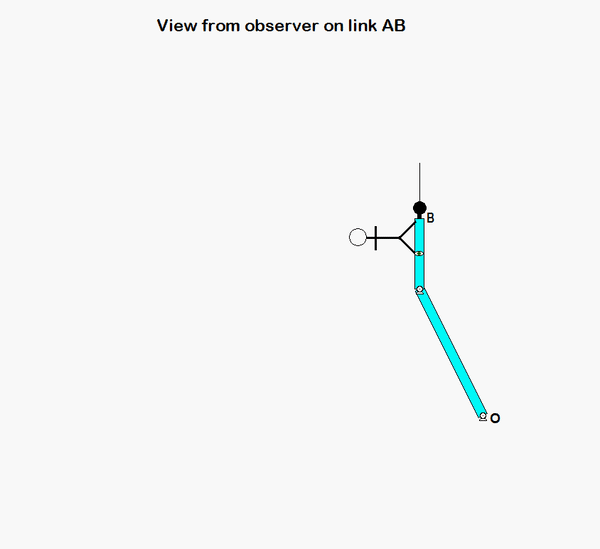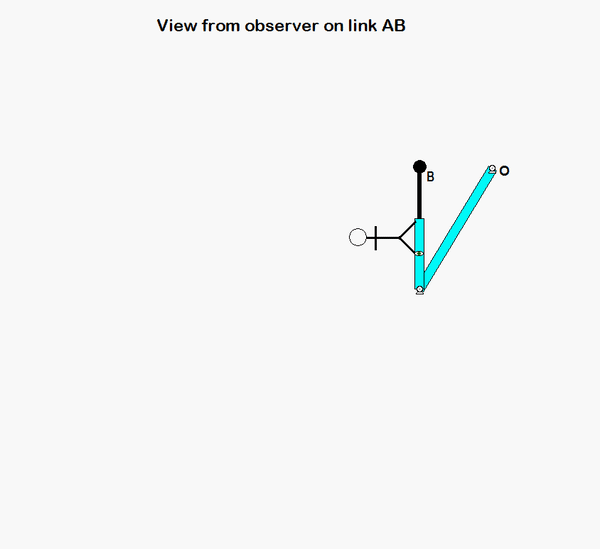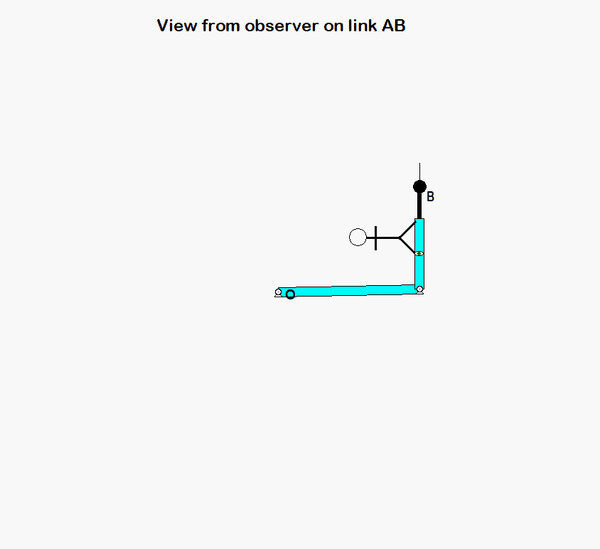
HINTS: The velocity of point B can be found from the following moving reference frame velocity equation:
vB = vA + (vB/A)rel + ω × rB/A
With the observer on link AD, we know the following:
vA = (L θ_dot) i
ω = φ_dot k
(vB/A)rel = b_dot i
Use similar logic for writing down the acceleration of B. Be careful in writing down the expression for aA ; in particular, aA ≠ 0. (A is traveling on a circular path with a constant speed.)