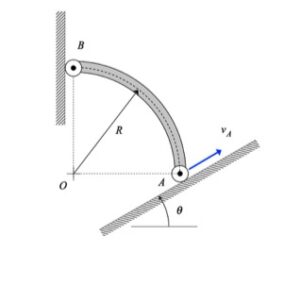
Discussion and hints:
The solution for the velocity and acceleration of end B is a straight-forward application of the rigid body velocity and acceleration equations for member AB:
vB = vA + omega x rB/A
aB = aA + α x rB/A - ω2*rB/A
where vB = vB*j, vA = vA*(cos(θ)*i + sin(θ)*j), aB = aB*j and aA = aA*(cos(θ)*i + sin(θ)*j). Each of the two vector equations above represents two scalar equations, providing us with the necessary equations to solve for vB, ω, aB and α.
HINT: The solution for this problem follows very closely that of Example 2.A.7 of the lecture book. If you get stuck on this problem, it is recommended that you review the solution video for Example 2.A.7 on the course website.
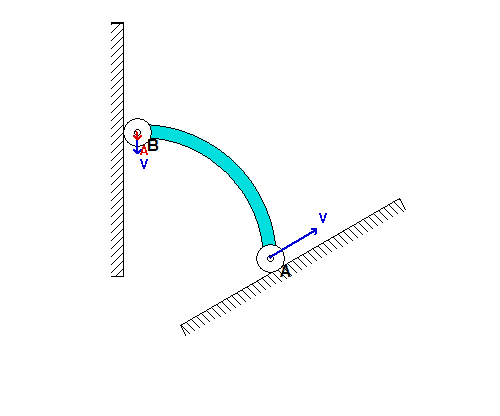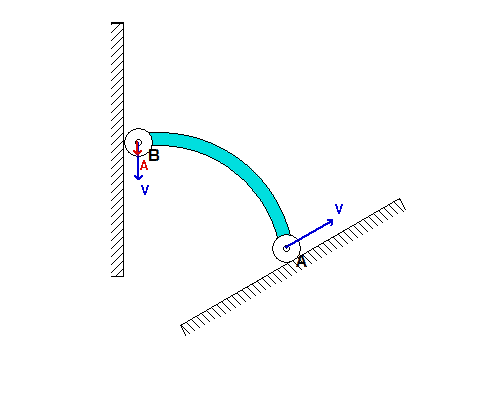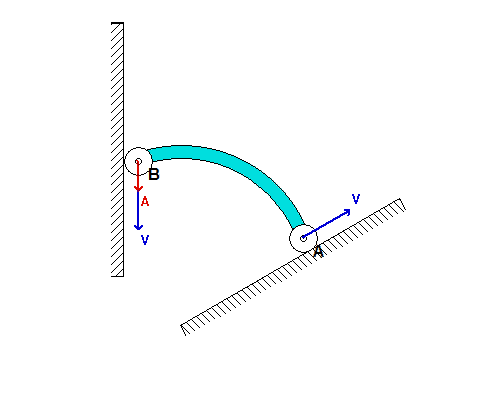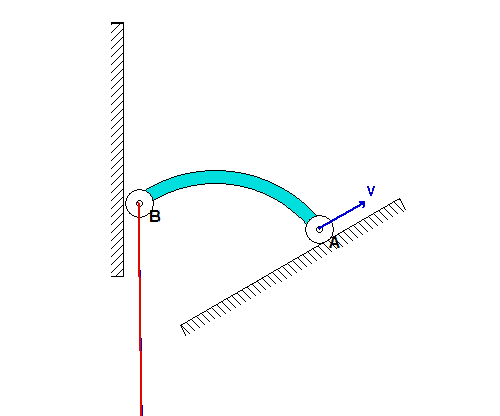
For the inclination angle used in the above simulation, we see that point B moves DOWNWARD along the vertical wall as A moves up along the incline. As B moves onto the same horizontal plane as A, the acceleration of B becomes very large (although A continues to move with a constant speed). Can you provide a physical explanation for this?

If we now consider a steeper inclination angle for A, as used above, we see that end B initially moves UPWARD along the wall; however, at some point B reverses its direction and begins to move DOWNWARD along the wall. Can you provide a physical explanation for this? Note also that the acceleration of B becomes very large as B moves onto the same horizontal plane as A, as it was for the initial value of inclination angle.
What is the value of the incline angle theta that defines the boundary between the types of initial motions for bar AB shown in the above two simulations? For the numerical value of the angle theta provided in the problem statement, which of the two simulations above agree with your results?
Any questions?? Please ask/answer questions regarding this homework problem through the "Leave a Comment" link above.