Discussion
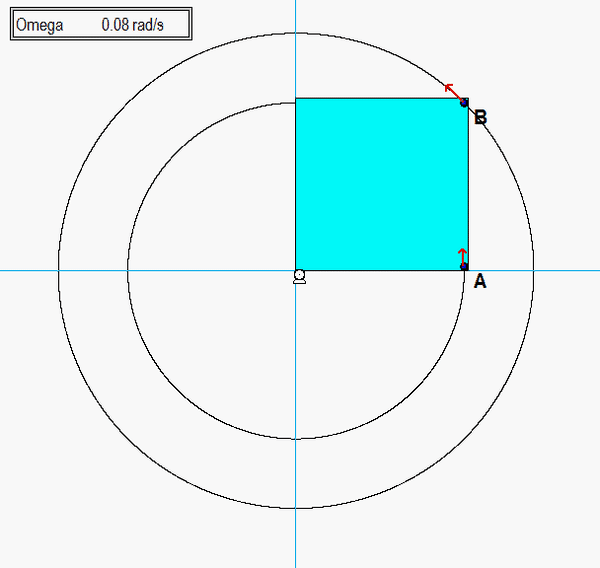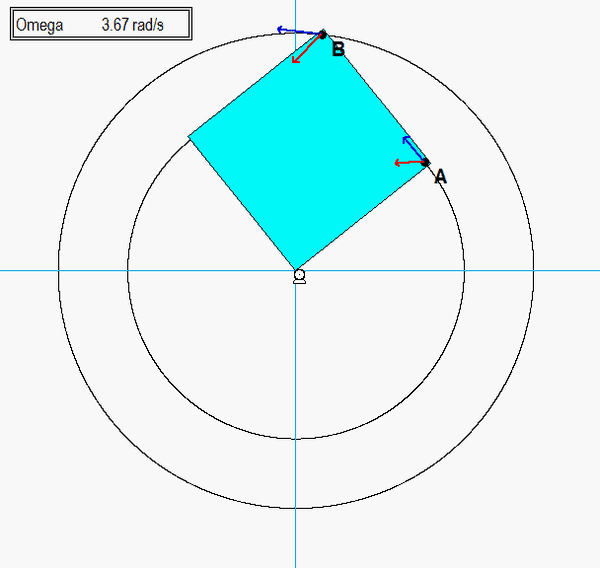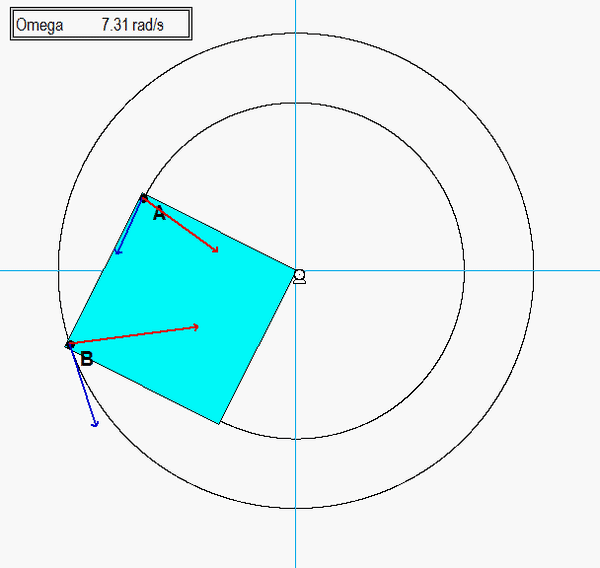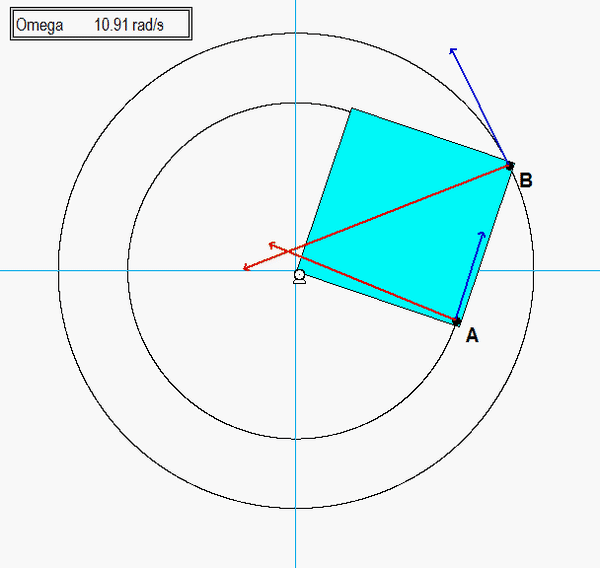
Note that the plate rotates about point O. Therefore, O is the center of the circular paths of points A and B. From the animation above, we see that the velocities of A and B are tangent to their circular paths, as expected. The accelerations of A and B are NOT perpendicular to the paths of A and B since the speeds of A and B are increasing in time (and consequently, A and B each have positive tangential components of acceleration).
Initially, the acceleration for these two points is nearly aligned with velocity, since the speeds are small and therefore the centripetal components of acceleration are small. Near the end of the first revolution of the plate, the speeds have increased to the point where the centripetal components of acceleration dominate, and acceleration is nearly perpendicular to the path.
Solution hints
For Part a) of this problem, it is recommended that you use the rigid body kinematics equations using point O as the reference point, since the velocity and acceleration of O are zero. That is, you should use v_B = v_O + Ω x r_B/O and a_B = a_O + Ω_dot x r_B/O - Ω^2*r_B/O. Repeat the process for finding the velocity and acceleration of A.
For Part b) of this problem, it is recommended that you use the rigid body kinematics equations with point A first. This will give you the equations needed to find Ω_dot. Then, use the rigid body kinematics equations to find the acceleration of B.
Any questions?? Please ask/answer questions regarding this homework problem through the "Leave a Comment" link above.